Comparative Study of First-Order Moving Asymptotes Optimizers for the Moving Morphable Components Topology Optimization Framework
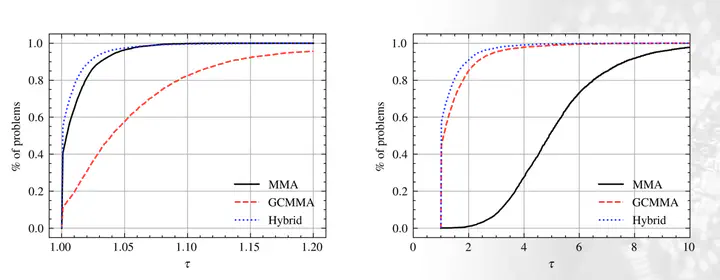 Image credit: Unsplash
Image credit: Unsplash
Abstract
Machine learning-accelerated topology optimization faces the challenge of generating large amounts of optimal topologies for supervised learning on a training dataset. This data generation step is challenging for the method of Moving Morphable Components (MMC) which presents an oscillatory behavior near local optimum that negatively affects its convergence speed and therefore present a high data generation cost. This paper presents a comparative study of the most-used first-order optimizers applied to minimum compliance problems under the MMC framework for topology optimization. The Method of Moving Asymptotes (MMA), its Globally Convergent version (GCMMA) and the hybrid MMA-GCMMA optimizer are compared using their final compliance and the total number of iterations until convergence as performance metrics. An extensive set of diversified boundary conditions for a rectangular beam minimum compliance problem is used as case study. The method of performance profiles is utilized to provide for each solver a probability distribution of outperforming its counterparts. Numerical results show that using a hybrid optimizer can accelerate the convergence speed of the MMC framework while still producing equally compliant topologies when compared to the MMA optimizer.